三门问题将所有情况排列开来得出的概率和正确答案不符求解释
三门问题，将所有情况排列开来，得出的概率和正确答案不符，求解释?
显然这不是“所有的情况”，你连基本的p3/3都没列齐不是吗？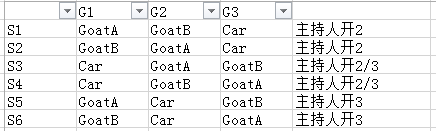
好吧，你既然展开了门和羊车的排列，那理所当然也一定能想到有这样6种情况
但是主持人没有开门3，所以S5 S6被排除了，对不对？
排除法，不是不能用，是需要正确地用——你也应该将S3 S4的随机概率除2才对嘛，对不对？
它们要被”排除一半“才是真正意义上的随机概率。
所以换到车的概率是 2 / (2+2/2)=2/3
不换拿到车的概率是（2/2）/（2+2/2）=1/3
我们不试图给门编号，这么考虑试试看：决定主持人开哪个门的，是你的初始选择
当你选了羊，这个概率是2/3，那么主持人只能替你排除掉一个羊，换来的必然是车
当你选了车，这个概率是1/3，那么主持人随便开一个门，你换就拿不到车
(其中开羊1门和羊2的概率是1/3下的两种对称情况，各自概率为1/3再除以2，是1/6，合计仍然为1/3）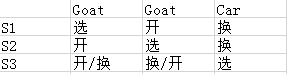
诺，换了就有车的情况是不是2/3?
或者说你这么告诉自己：
我选了羊，那换门就一定是车；我选了车，换门一定是羊
哟，你看，是不是换了拿车的概率还是2/3?
所以问题很简单，所有试图用编号解决问题的，都很容易会犯相同的错误——轻率排除而不是全部展开。
把主持人的人择当成了随机概率分布
或者你这么想，主持人也是随机开门，衍生一个特殊三门问题，那么是个什么情况：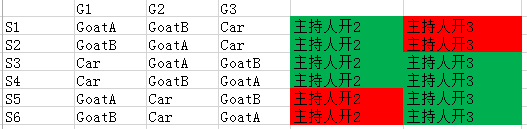
认真算算，如果是真正的概率事件，哪里有不同？
不同就在于红色部分是真的概率上的“未发生”，而不是人择
即：三个门之后有两羊一车，你随机选择一个门A之后，主持人从剩下的门B，门C里面随机开了一个，是羊，那么现在应该换还是不应该换呢？
如果是这个题面，那么显然换和不换各自是4/8
但是毫无疑问一般的三门问题，是以”主持人知道那扇门后面有车“为前提的
三门问题，将所有情况排列开来，得出的概率和正确答案不符，求解释?
Comments
Post a Comment